1. Two objects of different masses are dropped from rest. Neglect any effects due to air resistance (weight is the only force acting on the objects).
   • (A) The objects experience the same force and have the same acceleration.
   • (B) The objects experience different forces and have the same acceleration.
   • (C) The objects experience the same force and have different accelerations.
   • (D) The objects experience different forces and have different accelerations.
   • (E) The acceleration of the objects is 0.

2. An object of mass m (weight mg) is sitting at rest on a horizontal table-top. A spring scale is attached to the mass and is pulled vertically upward until it indicates that an upward vertical force of magnitude ½ mg is being exerted on the mass by the spring scale. The normal reaction force of the table-top on the mass is now:
   • (A) 0
   • (B) ½ mg
   • (C) mg
   • (D) 3mg/2
   • (E) dependent on other factors

3. A block of mass M is sliding on a friction-free plane inclined at an angle theta from the horizontal. The normal force exerted by the plane on the block is

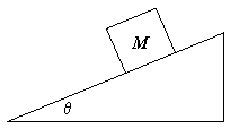   (A) g sin(theta) (B) Mg cos(theta) (C) Mg sin(theta) (D) Mg (E) 0

4. A box is given a push and released so that it slides across a rough horizontal surface. The magnitude of the acceleration of the box
   • (A) is directly proportional to the mass of the box.
   • (B) is inversely proportional to the mass of the box.
   • (C) is proportional to the square of the mass of the box.
   • (D) is proportional to the square root of the mass of the box.
   • (E) does not depend on the mass of the box.

5. A mass m is hanging from a string tied to the ceiling of an elevator. If the tension in the string is T and T > mg then:
   • (A) the elevator is at rest;
   • (B) the elevator is accelerating upward;
   • (C) the elevator is accelerating downward;
   • (D) the elevator is in free fall;
   • (E) the elevator is moving upward and decelerating.

6. Consider a ball tied to a string and being whirled in a horizontal circular path. In the following top-view diagram, which path best represents the one followed by the ball if the string breaks at point P?

   .

7. Which of the following statements concerning the speed of a satellite in a stable circular orbit around a planet is NOT correct?
   • (A) The orbital speed is determined by applying Newton's 2nd law to the satellite motion.
   • (B) The orbital speed depends on the radius of the orbit.
   • (C) The orbital speed depends on the satellite's height above the planet's surface.
   • (D) The orbital speed depends on the mass of the planet.
   • (E) The orbital speed depends on the mass of the satellite.

8. A woman pulls a crate up a rough inclined plane at constant speed. Which statement concerning this situation is NOT true?
   • (A) The gravitational potential energy of the crate is increasing.
   • (B) The net work done by all the forces acting on the crate is zero.
   • (C) The work done on the crate by the normal force of the plane is zero.
   • (D) The work done on the crate by gravity is zero.
   • (E) The woman does positive work in pulling the crate up the incline.

9. Two balls are dropped from the same height from the roof of a building. One ball has twice the mass of the other. When the balls reach the ground, how do the kinetic energies of the two balls compare? (Ignore any effects due to air resistance.)
   • (A) The lighter one has one fourth as much kinetic energy as the other.
   • (B) The lighter one has one half as much kinetic energy as the other.
   • (C) The lighter one has the same kinetic energy as the other.
   • (D) The lighter one has twice as much kinetic energy as the other.
   • (E) The lighter one has four times as much kinetic energy as the other.

10. Block 1 is released from rest at the top of a frictionless incline at a height h above the floor. Block 2 is dropped from rest, also from height h. Compare the speeds of the two blocks just before they reach the floor.
    • (A) speed of Block 1 > speed of Block 2.
    • (B) speed of Block 1 = speed of Block 2.
    • (C) speed of Block 1 < speed of Block 2.
    • (D) no statement can be made regarding the comparison of the blocks' speeds without knowing the angle of the incline.
    • (E) no statement can be made regarding the comparision of the blocks' speeds without knowing the value of h.

ANSWERS:

1. (B) - The weight force depends on mass (W = mg) so it is different, but the acceleration of each object is g, the acceleration due to free fall.
2. (B) - Since the upward applied force is less than the weight of the object, it does not move vertically. Therefore the net vertical force is 0, so the normal force has a magnitude of ½mg.
3. (B) - Choosing a coordinate system parallel and perpendicular to the plane, since the acceleration perpendicular to the plane is 0, the net force perpendicular to the plane is also 0. Therefore, the magnitude of the normal force equals the magnitude of the y component of the weight.
4. (E) - Choosing a coordinate system of horizontal and vertical axes, the only horizontal force is that of kinetic friction. In the vertical direction, 0 vertical acceleration means no net vertical force, and therefore the magnitude of the normal force equals the magnitude of the weight (mg). From Newton II, the acceleration of the box is the frictional force divided by the mass of the box. After substituting that the frictional force equals the normal force (mg) times the coefficient of kinetic friction, the acceleration is found to be the coefficient of kinetic friction times g, independent of the mass of the box.
5. (B) - Since the tension is greater than the weight there is a net upward force on the mass and hence an upward acceleration.
6. (B) - Since the ball's velocity is tangent to the circular path, when the string breaks the ball moves in a straight line tangent to the path at the point where the breakage occurs.
7. (E) - Applying Newton II, where the gravitational force of the planet on the satellite causes the required centripetal acceleration, the mass of the satellite appears to the first power on both sides of the equation, and so divides out.
8. (D) - Since gravity has a component along the plane, the work done on the crate by gravity is NOT zero.
9. (B) - Since air resistance effects are being ignored, mechanical energy is conserved. Being dropped from rest, the initial energy of each ball is all potential, mgh. When the balls reach the ground (h = 0) the energy is all kinetic (and equals mgh). Therefore the final kinetic energy is proportional to the mass of the ball.
10. (B) - Since the incline is frictionless, mechanical energy is conserved for both blocks. Since they both start from rest at the same height h, applying conservation of mechanical energy shows that they both have the same speed (square root of 2gh) just before reaching the floor.

Return to Resources Page