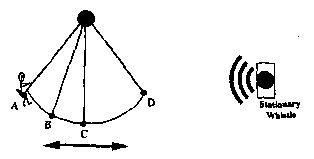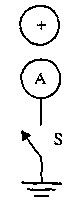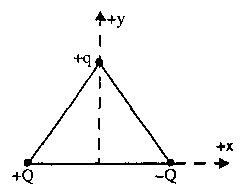Questions from April 1998 Physics 111 Final Examination

 

  A1.    A boy leaning over the edge of a cliff simultaneously throws two identical balls with the same speed.  One ball, A, is thrown vertically upward and the other ball, B, is thrown vertically downward.  Which one of the following statements is correct?

            (A)    Both balls hit the ground with the same speed and at the same time.

            (B)    Both balls hit the ground with the same speed, and ball B reaches the ground before ball A.

            (C)    Ball B hits the ground with a greater speed than ball A, and ball B reaches the ground before ball A.

            (D)    Ball B hits the ground with a greater speed than ball A, and both balls reach the ground at the same time.

            (E)    Ball B hits the ground with a greater speed than ball A, and ball A reaches the ground before ball B.

 

  A2.    Two objects constitute an isolated system.  In an elastic collision between the two objects, which one of the following is a FALSE statement?

            (A)    The total kinetic energy is conserved.

            (B)    The kinetic energy of each object is the same before and after the collision.

            (C)    The total momentum is conserved.

            (D)    The magnitude of the force exerted by each object on the other object is equal.

            (E)    The total kinetic energy before the collision is equal to the total kinetic energy after the collision.

 

  A3.    The solid wheel on a stationary exercise bicycle is rotating with a constant angular acceleration.  Which of the following statements is true?

            (A)    All points on the wheel have the same tangential acceleration.

            (B)    All points on the wheel have the same centripetal acceleration.

            (C)    At any instant, all points on the wheel have the same tangential velocity.

            (D)    At any instant, all points on the wheel have the same angular velocity.

            (E)    The centripetal acceleration of a particular point on the wheel increases linearly with time.

 

A4.      As a spinning figure skater pulls his arms closer to his body

            (A)    his angular momentum increases and his rotational kinetic energy remains constant.

            (B)    his angular momentum remains constant and his rotational kinetic energy increases.

            (C)    both his angular momentum and rotational kinetic energy remain constant.

            (D)    his angular momentum remains constant and his rotational kinetic energy decreases.

            (E)    both his angular momentum and rotational kinetic energy increase.

 

  A5.    An object which weighs 100 N floats on a lake with 3/4 of its volume beneath the surface of the water.  What is the magnitude of the buoyant force acting on the object?

            (A)  25 N      (B)  75 N      (C)  100 N      (D)  133 N      (E)  400 N

 

  A6.    A nonviscous incompressible fluid undergoes steady streamline flow through a horizontal pipe.  One section of the pipe is narrower than the rest.  When the fluid moves into the narrow section of the pipe

            (A)    the speed of the fluid increases and the pressure of the fluid decreases.

            (B)    both the speed of the fluid and the pressure of the fluid decrease.

            (C)    both the speed of the fluid and the pressure of the fluid increase.

            (D)    the speed of the fluid decreases and the pressure of the fluid increases.

            (E)    the speed of the fluid decreases and the pressure of the fluid does not change.

 

  A7.    A mass is attached to a spring on a horizontal, frictionless surface.  The mass is displaced to stretch the spring from its original unstretched length and then released.  It is observed to oscillate at a certain frequency.  In order to increase the frequency of the oscillatory motion, one could

            (A)    reduce the spring constant of the spring.

            (B)    replace the spring with a longer one of equal stiffness to the original one.

            (C)    decrease the mass on the end of the spring.

            (D)    reduce the distance that the spring is initially stretched.

            (E)    increase the distance that the spring is initially stretched.

 

  A8.    At a distance x from a sound source that is emitting constant power uniformly in all directions the sound intensity level is 90 dB.  At what distance from the source will the sound intensity be 70 dB?

            (A)  20 x     (B)  100 x     (C)  10 x     (D)  2 x     (E)  Ö20 x

 

A9.    The diagram at the right shows the various positions of a child in motion on a swing.  Somewhere in front of the child, a stationary whistle is blowing.  At which position(s) will the child hear the lowest frequency for the sound from the whistle?

 

            (A)    at both A and D

            (B)    at C when moving toward D

            (C)    at C when moving toward B

            (D)    at B when moving toward A

            (E)    at B when moving toward C.

 

A10.    A violinist is attempting to tune her instrument by listening for beats between a tuning fork and her instrument when one of its strings is bowed.  The violinist notices that the beat frequency decreases when the string is tightened slightly.  Which one of the following statements is correct?

            (A)    The violin string frequency was initially lower than that of the tuning fork and becomes even lower when the string is tightened.

            (B)    The violin string frequency was initially lower than that of the tuning fork and approaches that of the tuning fork when the string is tightened.

            (C)    The violin string frequency was initially higher than that of the tuning fork and becomes even higher when the string is tightened.

            (D)    The violin string frequency was initially higher than that of the tuning fork and approaches that of the tuning fork when the string is tightened.

            (E)    The violin string cannot be tuned by using beats, since the beat frequency is not related to the frequencies of the string and tuning fork.

 

A11.    A positively charged sphere is brought near the top of an uncharged conducting sphere, A, which is connected to ground via the switch, S, as shown.  The switch is closed, then opened again, and then the charged sphere is removed.  The sphere A             (A)    is now positively charged.             (B)    is now negatively charged.             (C)    remains uncharged.             (D)    has a negative charge near the top and a positive charge near the bottom.             (E)    may have a positive charge, a negative charge, or no charge - it is impossible to tell.

 

A12.    Three charges, +q, +Q, and –Q, are placed at the corners of an equilateral triangle as shown.  The net force on the charge +q             (A)    points in the +y direction.             (B)    points in the –y direction.             (C)    is zero.             (D)    points in the +x direction.             (E)    points in the –x direction.

 

A13.    The magnetic force on a charged particle is:

            (A)    perpendicular to the direction of the particle’s motion and perpendicular to the direction of the magnetic field.

            (B)    perpendicular to the direction of the particle’s motion and parallel to the direction of the magnetic field.

            (C)    parallel to the direction of the particle’s motion and perpendicular to the direction of the magnetic field.

            (D)    independent of the relative directions of the magnetic field and the particle’s motion.

            (E)    independent of the magnitude of the particle’s charge.

 

A14.    An object is placed between the focal point and the surface of a spherical, concave mirror.  The resulting image is best described as

            (A)    real, inverted and enlarged.

            (B)    real, inverted and reduced.

            (C)    virtual, erect and reduced.

            (D)    virtual, erect and enlarged.

            (E)    real, erect and enlarged.

 

A15.    A scuba diver looking from under the water sees the sun at an angle of 20° from the vertical.  For an observer standing on the shore

            (A)    the sun’s rays make an angle with the vertical that is smaller than 20°.

            (B)    the sun appears to be higher than 70° above the horizon.

            (C)    the sun is vertically overhead.

            (D)    the sun appears to be lower than 70° above the horizon.

            (E)    the sun appears to be exactly 70° above the horizon.

 

A16.    Which one of the following statements is the assumption that Niels Bohr made about the angular momentum of the electron in the hydrogen atom?

            (A)    The angular momentum of the electron is zero.

            (B)    The angular momentum can assume only certain discrete values.

            (C)    Angular momentum is not quantized.

            (D)    The angular momentum can assume any value greater than zero because it's proportional to the radius of the orbit.

            (E)    The angular momentum is independent of the mass of the electron.

 

A17.    The minimum wavelength of the radiation emitted by an X-ray tube is determined by

            (A)    the dimensions of the tube.

            (B)    the difference in potential between the anode and the cathode.

            (C)    the intensity of the electron current hitting the anode.

            (D)    the mass of the photoelectrons.

            (E)    the wavelength of the light falling on the anode.

 

A18.    In the condition known as population inversion,

            (A)    the amount of one type of gas atoms is larger than that of another in a mixture.

            (B)    the number of energy levels that are populated is larger than that of unpopulated levels.

            (C)    there are more electrons occupying lower energy levels than occupying higher energy levels.

            (D)    there are more electrons occupying higher energy levels than occupying lower energy levels.

            (E)    there are more photons than electrons in a given system.

 

A19.    In a fission reactor, the purpose of the moderator is to

            (A)    absorb neutrons and hence slow the reaction down.

            (B)    carry energy to the turbines that generate the electricity.

            (C)    prevent radioactive material from contaminating the fuel rods.

            (D)    increase the chance that neutrons will cause fission reactions.

            (E)    allow the reactor to be used as a fusion reactor if desired.

 

A20.    Consider the following nuclear decay:  ²³⁶₉₂U ® ²³²₉₀Th + X

            If the uranium nucleus is at rest before its decay, which one of the following statements is true concerning the decay products:

            (A)    They have equal kinetic energies and momenta of equal magnitudes.

            (B)    They have equal kinetic energies, but X has much more momentum.

            (C)    They have momenta of equal magnitudes, but X has much more kinetic energy.

            (D)    They have equal kinetic energies, but the thorium nucleus has much more momentum.

            (E)    They have momenta of equal magnitudes, but the thorium nucleus has much more kinetic energy.

 

B1.    Calculate the maximum height reached by a baseball projected from a flat surface on the earth with an initial speed of 45.0 m/s at angle of 35.0° to the horizontal.  Neglect any effects due to air resistance.

 

B2.    A box of mass 2.00 kg is being pulled along a horizontal surface by a horizontal rope.  The tension in the rope is 5.00 N and the coefficient of kinetic friction between the box and the surface is 0.150.  Calculate the acceleration of the box.

 

B3.    An 80.0 kg man and a boy stand on the ends of a balanced, massless teeter-totter.  The fulcrum of the teeter-totter is located 1.50 m away from the man and 5.75 m away from the boy.  If the teeter-totter remains balanced, calculate the mass of the boy.

 

B4.    A pipe of length 12.0 m and radius 0.150 m is used to carry water (density of 1000 kg/m³, viscosity of 1.25 ´ 10^–3 Pa×s).  Calculate the pressure differential that must be applied across the ends of the pipe to obtain a volume flow rate of 0.140 m³/s.

 

B5.    Transverse standing waves of frequency 60.0 Hz are generated along a stretched wire of mass 0.0250 kg and length 1.25 m that is fixed at both ends.  Two antinodes are observed to exist between the fixed ends.  Calculate the tension in the string.

 

B6.    A proton is released from rest in an electric field of magnitude 1.30 ´ 10³ N/C.  Calculate the magnitude of the acceleration experienced by the proton.

 

B7.    An elderly man has perfect distance vision but can read a newspaper only when it is at least 60.0 cm from his eyes.  Calculate the refractive power (in diopters) of the contact lenses that will enable him to read a newspaper held 25.0 cm from his eyes.

 

B8.    A diffraction grating has 6000 slits per cm and is illuminated with light of wavelength 628 nm.  Calculate the angle, measured from the normal, at which the first order maximum will be observed.

 

B9.    The half-life of radioactive ¹⁴C is 5730 years.  An animal bone discovered in a cave is found to have only 70.0% of the number of ¹⁴C atoms per gram of carbon in a living bone.  Calculate the time since the death of the animal.

 

B10.  Calculate the energy (in MeV) liberated in the fusion reaction ²H + ³H ® ⁴He + n

         (Atomic masses:  ²H - 2.01410 u;  ³H - 3.01605 u;  ⁴He - 4.00260 u)

 

C1.   The starship, USS Enterprise, is in a stable, circular, gravitational orbit around a newly discovered planet.  The Enterprise completes 9.50 revolutions about the planet in 24.0 h when the ship is located 5.60 × 10⁶ m above the planet’s surface.  Sensors show that the planet has a mass of 6.50 × 10²⁵ kg.

         (a) Calculate the magnitude of the angular velocity of the Enterprise about the planet.

         (b) Calculate the radius of the planet.

         (c) Assuming that the planet is spherical and has a rotational period of 34.8 h, calculate the angular momentum of the planet about its rotation axis.

 

C2.   The real battery shown has an emf, V, of 9.00 V and an internal resistance, r, of 5.00 W.  It is to be connected to the network of resistors shown in the diagram.  In this network,

         R₁ = 35.0 W and R₂ = 60.0 W.

 

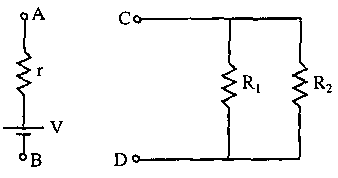         (a)  Calculate the equivalent resistance between the terminals C and D of the resistor network.

         (b)  When the battery terminal A is connected to C, and the battery terminal B is connected to D, calculate the current drawn from the battery.

         (c)  With the circuit connected as in (b) calculate the terminal potential difference of the battery (i.e. calculate the potential difference between A and B).

         (d)  With the circuit connected as in (b) calculate the current passing through the resistor R₁.

 

C3.   When a surface is irradiated with light of wavelength 511 nm, electrons are ejected from the surface with a maximum kinetic energy of 0.600 eV.  When a second source of light of unknown wavelength is used it is found that the emitted electrons have a maximum kinetic energy of 1.10 eV.

         (a)  Calculate the energy (in eV) in each photon of the light with wavelength 511 nm.

         (b)  Calculate the wavelength of the unknown light source.